In a teaching course I am taking I had to do a ten minute talk about anything, but it should be related to my research. The people listening to the talk was a mix of PhD students from different departments at my university. So I had to keep it simple enough so even people with weak mathematical backgrounds could understand what I was talking about. Most of the people did some slides explaining why they are interested in the subject they are doing their PhD in, which is fine but is sort of the easy path out. I thought about doing the same at first but figured a more fun exercise would be to show a proof on the black board. It is not much you can do in ten minutes so I settled for indirectly formulating Bayes’ Theorem, so here goes:

Cricket players and pints

Imagine you are an advertising person for the cricket federation and you wanna figure out if a possible advertising campaign for getting people to attend cricket games more could target people at pubs. And so you want to find out the probability of people who like a pint at the local pub also liking a game of cricket. Sure you could just do a survey, but surveys cost money and you just want to find an initial guess as to wether this would be an interesting survey to carry out. So we if we write down the two configurations we like to research/model:

A = I like cricket.
B = I like beer.

Now what we want to find out is:

P(A|B) = The probability of a person liking cricket given that he/she likes beer

We realize that going around asking everyone if they like beer and then in turn asking them if they like cricket would be quite cumbersome. There is lots of pubs in Britain! What if we could ask people that like cricket if they like beer? That is a much smaller subset since we could just ask people at games if they like beer taking for granted that they fancy cricket. We could even figure it out by doing something with the sales figures for beers at the games. So now we have

P(B|A) = The probability of a person liking beer given that he/she likes cricket

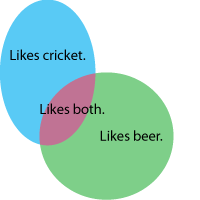
Now if we stop and ask ourself what is it that we are trying to calculate here? Lets draw the two possible events as intersecting circles(a Venn diagram) like this:

So actually what we are trying to find out is what subset of the beer circle that likes cricket i.e. the intersection in the Venn diagram. With (Venn) digrams one has to be careful about what they really mean. They are more meant as a visual aid, for example we could also easily equally correct interpret the intersection as the subset of the cricket likers that also like beers. But in our model we already knew who liked beers so we are dealing with the probabilities over the population that likes beers.

Now that we have some idea about what we really want we could try to be a bit more specific. Had we had some numbers we would have written for the probability of the intersection

P(A,B) = Number of people who like beer and cricket / Total population

And for the probability of beer likers we could write

P(B) = Number of people that likes beers / Total population.

Now if we want to formulate the conditional probability P(A|B) we could write it as

P(A|B) = (Number of people who like beer and cricket / Total population) / (Number of people that likes beers / Total population)

So the total population cancels out in the denominator and numerator for P(B|A). So what we need to write is actually just

P(A|B) = P(A,B) / P(B)

So we are almost there, the only question is how do we model P(A,B)? P(A|B) was costly to model so P(A,B) should not be much cheaper. But what about P(B|A), that was less costly. Could we rewrite P(A,B) in terms of P(B|A)? It turns out that we can! If we write it out

Number of people who like beer and cricket / Total population = (Number of people that like beer that also like cricket / Number of people that likes cricket) * ( Number of people that likes cricket / Total population)

So basically what we are saying here is that given our total population the probability that people like both beers and cricket is the same as that of the probability that people who like cricket also likes beer multiplied by the probability that person likes cricket. We could view this as an elimination process – first we pick out the cricket likers from the total population and then from these we pick out the beer likers. Formally we write

P(A,B) = P(B|A) P(A)

And so finally if we put it all together we get

Bayes’ Theorem: P(A|B) = P(B|A) P(A) / P(B)

And we now have a notion of the probability of a person liking cricket given that he/she likes beer and wether not we should carry out that survey we wanted to evaluate.